Împerecherea - desen tehnic

Conjugarea numit pentru o tranziție lină de la o Do-SRI la o altă curbă. Mates sunt circulare și catenă lineară. Construirea ei se bazează pe proprietățile tangentelor liniilor curbe. Conjugarea segmentelor de linie cu curbele circulare vor fi posibile în cazul în care punctul de cuplare este, de asemenea, punctul de tangență al curbei unui arc drept. Prin urmare, raza de racordare trebuie să fie perpendiku-lar la linia de la punctul de tangență.

Împerecherea curbele circulare este posibilă atunci când punctul de cuplare va fi în același timp și punctul de contact al arcurilor conjugate. Prin urmare, punctul de atingere ar trebui să fie pe linia de centrele arcelor de cercuri.

Împerecherea linii intersectate:

Exemplul 1. Date fiind intersectând linii drepte AB și BC și raza-conjugarea cu R; necesită pereche de linii (fig. 66, a, b, c).

Conjugarea este posibil, în cazul în care liniile AB si BC-TION va fi tangenta la cercul de rază R. Pentru a găsi centrul cercului

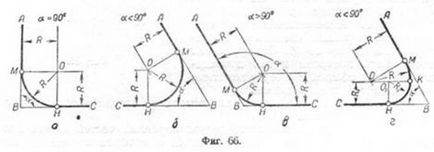
se efectuează la o distanță R paralelă cu liniile drepte predeterminate pentru a sprijini traversarea lor reciprocă la 0. Din punctul O ca centru, este raza arcului realizează R. Punctele de conjugare va punctul M și H sunt definite de intersecția liniilor drepte AB și BC cu ei coborât perpendicularele din punctul O.

Exemplul 2. Date fiind intersectând linii drepte AB și BC și razele R și R1 conjugare conjugare Construcția este posibilă dacă unghiul a<90.

O metodă de construire a unei astfel de asociere este prezentată în Fig. 66 g.

linii paralele împerecherea

Exemplul 1. Având în vedere două linii drepte paralele AB și interfața CE și punctele B și C (fig. 67).

Este necesar să se construiască curbele de amestecare circulară, astfel încât să treacă prin punctele specificate K, în mijlocul segmentului BC.

Pentru a determina raza și centrul de împerechere arce împart segmente de linii BK și CS, astfel încât acestea sunt perpendiculare pe aceste segmente și le-a împărțit în jumătate. Deoarece raza de racordare trebuie să fie perpendicular pe linia de la punctul de cuplare, apoi pentru a găsi centrele O arce de interfață restabili punctele B și C perpendi-kulyary până la intersecția lor cu perpendiculare efectuate anterior la linia BC.

Punctele de intersecție ale acestor perpendicularele determina poziția interfețelor centrului O-O, precum și între segmentele 05 și valoarea FLS OS da din raza de racordare.

Exemplul 2. (fig. 68) Acest exemplu este diferit de cel anterior

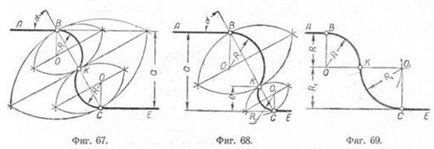
faptul că punctul de a lua de pe linia BC la întâmplare, la o adresă de e-picioare dis de linia CE; Prin urmare, raza R file și R1- dimensiuni diferite. Proceedings de construire conjugat este aceeași ca și în exemplul de pre-anterior.

N și m e p p 3. Dată: distanța dintre două linii paralele, și EC mymi AB egal cu suma razei R conjugată și R1, iar punctul de cuplare B (fig 69.).

Pentru a construi conjugare efectua în paralel cu distanța AB-SRI R linie auxiliară 0-01. Centrul pentru conjugarea 0-ra raza R va fi amplasat la intersecția perpendiculara conected-TION din punctul B la linia auxiliară. Descriind din raza O arc R, găsiți K punct, din care raza R1 de a face unui auxiliar drept crestătură definind centrul de împerechere O1. Din punctul O1 pe o linie dreaptă perpendiculară pe omită CE și găsirea punctului conjugat zheniya-C punctul K și interfațat cu arc de rază R1.

Conjugarea cu arc drept

Exemplul 1. Construct conjugarea arc cu raza R cu o directă AB raza R1 (fig. 70). Pentru a face acest lucru, găsiți centrul interfață 0 și interfața de puncte C și o. Punctul C este, de asemenea, punctul de tangență și trebuie să se afle pe linia de centre de arce. Raza de conjugat-TION trebuie să fie perpendicular pe linia AB la punctul de contact a. Prin urmare, din centrul O descrie ra-rază egală cu suma R + R1, arc.

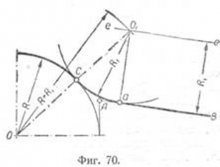
Acesta va fi centrul de conjugare-0, pentru a determina Koto-cerned au fost efectuate în paralel la o distanță R1 AB filială directă inlantuiti ei la intersecția cu arc CHECK donnoy. Punct Combinarea O1 și O, găsim punctul de conjugare C. Pentru determinarea punctului și omite din O1 perpendicular AB. Mai departe, raza R1 din centrul O1 al conjugarea a și S.

Exemplul 2. Date fiind: o rază R arc, linia AB și un punct-TION și conjugare. este necesară Conjugarea pentru a găsi punctul C și raza de racordare R1 (fig. 71). Cheltuielile prin punctul și perpendicular pe AB, care otklady segmentul de jos Du- aK, R. egal care unește centrul O de la punctul K. Pentru a găsi asocierea prin centrul O1 așteptare punctul de mijloc linie perpendiculară pe OK, care traversează direct Ak la punctul O1 O1 Combinarea cu O, vom găsi punctul de co-conjugarea S.

arce de conjugare arc de cerc

Conjugarea arce mo-Jette fi extern (fig. 72) sau frecare ADNurile (fig. 73). In ambele cazuri, conjugare sunt fezabile: 1) cursa de-distanța C între O și 01 centre de arce conjugate mai mari decât suma R lor raze și R1 (Figura 72a și 73 a), respectiv. C> R + R1 + 2) unde C= C + R1 sau R1> = C + R. Pentru arce de interfață externă conjugare ar, de asemenea, nu este posibil în cazul în care raza arcului R2 a dispozitivului de cuplare va fi mai mică de jumătate de C - .. (R + R1), adică R2 <

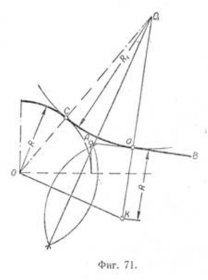
<(C-(R+R1))/2. Во всех случаях решение за-дачи сводится к на-хождению центра 02 сопрягающей дуги ра-диуса R2 и точек со-пряжения A и В.

Extern set-conjugat. Sunt: (fig. 72, a) cos-arc raze R și R1-set distanța C dintre centrele arcurilor și raza co-conjugare R2. Conjugarea este necesară pentru a construi condiție Wii care C> R + R1.

Pentru a construi cuplajul necesar pentru a determina punctul central 02 și cuplarea A și B. Pentru determinarea centrului de susținere 02 al centrului O razei arcului R2 + R, un centru O1 al arcului de rază R2 + R1 intersecție dintre aceste muchii definesc centrul drepte 02. Combinarea Centre O și 01 cu centrul 02, pentru a găsi intersecția acestor linii cu respectivul cuplaj arce punctul a și punctul B. rezultată raza interfațat R2.

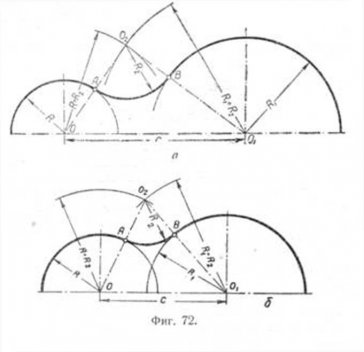
Interfețele de construcții pentru cazul în care C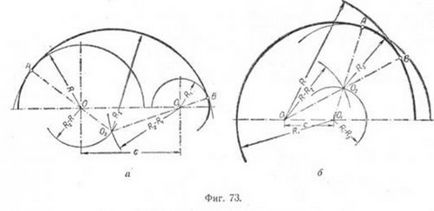

conjugarea internă. Sunt: R și R1 arc raze distanță C dintre centrele arcurilor și raza de racordare R2 (Figura 73, precum și.). Tre-Buet construi o pereche, în cazul în care soluția C> R + R1 la această problemă este aceeași ca și cea precedentă, cu singura diferență fiind că centrele O și O1 a avut loc raza arcului R2 - R și R2 - R1.

FIG. 73 b prezintă construcția conjugare pentru cazul în care C