Unghiul Trigonometrie - unghiul de rotație

În trigonometria concept important este unghiul de rotație. Mai jos vom oferi în mod constant o imagine pe turn și introduceți toate conceptele aferente. Să începem cu o idee generală de cotitură, spune despre o revoluție completă. În continuare proceda la conceptul de unghiul de rotație și de a examina caracteristicile sale, cum ar fi direcția și cantitatea de rotație. În cele din urmă, definim cifra de rotație în jurul unui punct. Întreaga teorie a textului va oferi exemple și ilustrații grafice explicative.

Navigare în pagină.

Ceea ce se numește un punct de cotitură în jurul punctului?

Acum, observăm că, împreună cu fraza „rândul său, în jurul punctului“ se va folosi, de asemenea, expresia „rândul său, despre punctul“ și „punctul de rotație relativă“, ceea ce înseamnă același lucru.

Noi introducem conceptul de punctul de cotitură în jurul punctului.

Mai întâi vom defini centrul de rotație.

Punctul despre care se realizează rotația, se numește centrul de rotație.

Acum, să spunem că este rezultatul unui punct de cotitură.

Ca urmare a rotației unui punct A în raport cu punctul O centrul de rotație se obține A1 (care, în cazul unui număr de rotații complete, poate coincide cu A), în care A1 se află pe un cerc cu centrul la raza O OA. Cu alte cuvinte, atunci când se rotească în jurul punctului O mută punctul A la punctul A1. situată pe un cerc centrat pe punctul de rază O OA.

Se crede că în punctul O este rotit în jurul valorii de sine, pornește în sine. Aceasta este, prin rotație în jurul punctului central de rotație O O trece în sine.

De asemenea, demn de remarcat este faptul că punctul de rotație A în jurul punctului O este considerată ca mișcarea de mișcarea punctului A de pe circumferință cu centrul în punctul de rază O OA.

Pentru claritate, o ilustrare a punctului de pivotare în jurul unui punct O. A în figura de mai jos, deplasarea punctului A la A1 arată punctul prin săgeți.

rotație completă

Se poate efectua un astfel de punct de rotație A în raport cu centrul de rotație O. A. treacăt că punctul toate punctele de cerc, va fi pe același loc. În același timp, se spune că punctul A a făcut o revoluție completă în jurul punctului O.

Să ne dea o ilustrare grafică a cifrei de afaceri totală.

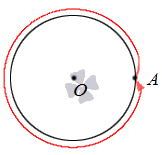
Dacă nu se opresc la o revoluție, și să continue să se deplaseze la punctul de cerc, este posibil să se efectueze două, trei și așa mai departe cu viteză maximă. În figură, dreapta jos arată cum două rotații complete, iar stânga poate fi produs - trei ture.

De asemenea, puteți vorbi despre părțile unei rotații complete, de exemplu, aproximativ jumătate din cifra de afaceri, al treilea, al patrulea, etc. rândul său, (dacă este necesar, a se vedea articolul și cota fracțiuni comune).

Conceptul de unghiul de rotație

Dintr-o în primul introdus paragraf concepte punctul de pivot, este clar că există infinit mai multe variante de un pivot în jurul punctului O. Într-adevăr, orice punct al circumferinței cu centrul în raza OA O punct poate fi considerat ca fiind punctul A1. rezultă punctul pivot A. De aceea, pentru a distinge unul de altul rândul său, introduce conceptul de unghiul de rotație.

O caracteristică a unghiului de rotație este direcția de rotație. În direcția de rotație este judecat cu privire la modul de a pune în aplicare punctul de rotație - sensul acelor de ceasornic sau în sens invers.

O altă caracteristică a unghiului de rotație este valoarea sa. Unghiurile de rotație sunt măsurate în aceleași unități ca unghiurile în geometrie. cele mai frecvente grade și radiani. Aici este de remarcat faptul că unghiul de rotație în grade poate fi exprimată de către orice număr real în intervalul de la minus infinit la infinit plus, spre deosebire de geometrie unghi a cărui valoare este pozitivă în grade și nu depășește 180.

Pentru a indica unghiurile de rotație sunt utilizate în mod obișnuit litere mici ale alfabetului grecesc, etc. cu o singură literă subscript sunt adesea folosite pentru a desemna un număr mare de unghiuri de rotație, de exemplu.

Acum să vorbim despre caracteristicile unghiului de rotație, și mai mult în ordine.

Direcția de rotație

Lăsați un cerc centrat la punctul O punctul A marcat și A1. Punctul A1 se poate obține de la punctul A. să se rotească în jurul centrului de O, fie în sens orar sau - invers acelor de ceasornic. Aceste entorse logice să se gândească diferit.

De acord să ia în considerare o rotație în direcția pozitivă a unui viraj, care se realizează în sens antiorar. rotatie contrar acelor de ceasornic se numește rotație în direcția negativă.

Ilustrarea rotații în direcțiile pozitive și negative. Figura de mai jos prezintă un viraj la stânga în direcția pozitivă, iar dreapta - negativ.

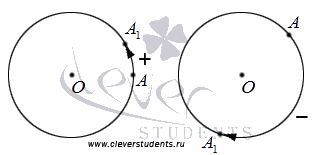
Mărimea unghiului de rotație, unghiul de magnitudine arbitrar

Corner punct de pivot diferit de centrul de rotație, este complet determinată de o indicație a valorii sale, pe de altă parte, magnitudinea unghiului de rotație poate fi judecat pe modul în care această modificare a fost efectuată.

Așa cum am menționat mai sus, mărimea unghiului de rotație în grade, exprimată ca numărul de -∞ la + ∞. Aici semnul plus corespunde o rotație în sensul acelor de ceasornic, iar semnul minus - rotiți în sens antiorar.

Acum trebuie să se stabilească o corespondență între mărimea unghiului de direcție și astfel încât unele rândul său, acesta corespunde.

Începem cu unghiul de rotație de zero grade. Acest unghi de rotire corespunde deplasării punctului A la sine. Cu alte cuvinte, atunci când este rotit 0 grade în jurul punctului A punctul O rămâne în loc.

Mai departe spre rândul său, în jurul punctului O. Un punct în care rotația are loc într-o jumătate de revoluție. Presupunem că punctul A se mută la punctul A1. În acest caz, valoarea absolută a unghiului în grade nu AOA1 depășește 180. În cazul în care rotația este în direcția pozitivă, valoarea unghiului de rotație este considerat egal cu AOA1 unghi. iar dacă rotația este într-o direcție negativă, atunci valoarea sa este considerată a fi egală cu AOA1 unghi negativ. De exemplu, să ilustrare prezentând unghiuri de rotație de 30 180 și -150 grade.

Rotație unghiuri de înclinare mai mare de 180 de grade și mai puțin de -180 de grade determinate pe baza următoarelor proprietăți rotații succesive destul evidente. mai multe rotații succesive cu privire la punctul central A O echivalent cu o rotire, magnitudinea care este egală cu suma valorilor acestor rotații.

Iată un exemplu care ilustrează această proprietate. Pentru a roti în raport cu punctul A punctul O de 45 de grade, iar apoi acest punct încă se rotesc la 60 de grade și apoi rotiți acest punct de -35 grade. Notăm aceste puncte intermediare la ambele colțuri A1. A2 și A3. În același punct A3 am putea obține urmând un punct de rotație A, la un unghi de 45 + 60 + (- 35) = 70 de grade.

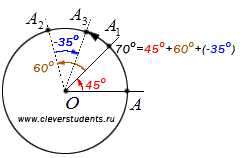
Astfel, unghiurile de rotație, mai mare de 180 de grade, vom prezenta câteva rotații consecutive la colțuri, care dă suma valorii unghiului inițial de rotație. De exemplu, unghiul de rotație de 279 de grade corespunde rotații succesive de 99 și 180 de grade, sau 90 și 90. 90. 9 grade, sau 180 la 180 și -81 grade sau 279 rotații consecutive la 1 grad.

In mod similar determinate și de rotație unghiuri mai mică de -180 de grade. De exemplu, unghiul de rotație de -520 de grade poate fi interpretată ca un punct de cotitură secvențială -180. -180 și -160 de grade.

Pentru a rezuma. Am determinat unghiul de rotație, a cărui valoare este exprimată în grade unele număr real în intervalul de la -∞ la + ∞. În trigonometria, vom lucra în mod specific cu unghiurile de rotație, deși cuvântul „turn“ este adesea omis, și pur și simplu spune „unghi“. Astfel, în trigonometria, vom lucra cu unghiuri arbitrar mari, prin care se înțelege unghiurile de rotație.

Pentru a încheia această secțiune, observăm că rotire completă corespunde unghiului de rotație de 360 ​​de grade în direcția pozitivă (sau 2 · tt radiani), iar în negativ - unghiul de rotație la -360 grade (sau -2 · π rad). Este convenabil să reprezinte unghiuri mai mari de rotație ca un anumit număr de rotații complete și o altă rotație printr-o valoare a unghiului de la -180 la 180 de grade. De exemplu, ia în considerare unghiul de rotație 1340 grade. Easy 1340 reprezentat ca 4 · 360 + (- 100). Adică, unghiul inițial de rotație corespunde cu 4 rotații complete într-o direcție pozitivă și rândul său, ulterior -100 de grade. Un alt exemplu -745 de grade unghi de rotație poate fi interpretat ca două rotații în sens antiorar și rotația ulterioară de -25 grade, ca -745 = (- 360) + 2 · (- 25).

figura de rotație în jurul unui punct de unghi

Conceptul de pivot punct poate fi ușor extins pentru a se roti în jurul orice figura pe unghiul punctului (este vorba de o astfel de rotație ca punctul care se realizează rotația și figura, care este rotit pentru a se afla într-un singur plan).

Prin rotirea cifrele ne referim la toate punctele rândul său, forma în jurul unui punct predeterminat, la un anumit unghi.

Ca un exemplu, următorul grafic: executa un segment de întoarcere AB la un unghi în raport cu punctul O. Acest segment atunci când cotitură mișcare în segmentul A1 B1.