Asocierea directă cu cercul

În general, construcția de cuplare circumferențiale m R1 și linia raza cercului l de rază R (. Fig.30 a, b) după cum urmează:

- la o distanță R conductor paralel l l „(GM la linie);

- cu centrul la O1 petrece m „(GM la un cerc), cu o rază egală cu suma R și R1 sau egală cu raza R diferența și R1;

- punctul O de intersecție l „și m“ este interfața hub;

- omite de la O perpendicular pe linia l. Se obține punctul conjugare A;

- O1 prin O și efectua în mod direct și nota de împerechere punctul de intersecție cu cercul m;

- cu centrul în punctul O de rază R între punctele A și B efectua arc împerechere.

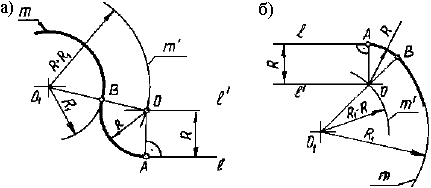
Fig. 30. Construcția liniei drepte conjugare cu cercul

Asocierea a două cercuri

În construcția interfeței externe a două m1 cercuri și arcul m2 pe o rază predeterminată R (Fig.31) Centrul arcului imperechere - punctul O - determinată de intersecția a două m1 loci „și m2“ - cercurile auxiliare ale razelor R + R1 și R + R2. a avut loc, respectiv, din centrele de contact ale cercurilor, adică, din punctele O1 și O2. punctele de cuplare A și B se determină ca punctul de intersecție al setului de cercuri cu OO1 drepte și oo2.

Perechea interioară R1 și R2 razelor de arce de arc raza R este prezentat în Fig. 32.

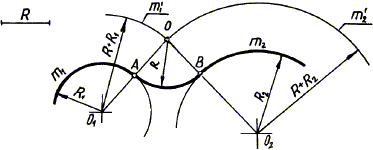
Fig. interfațare 31. externe două cercuri

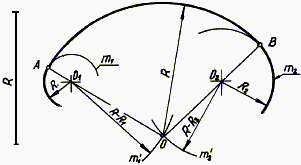
Fig. 32. Perechea interioară a două cercuri

Pentru a determina centrul O al arcului efectuarea conjugării punctelor O1 și O2 arc auxiliar m1 „și m2“ - două spațiu geometric - razele R-R1 și R-R2. Punctul de intersecție al acestor arce este o conjugare centru. Din punctul O prin punctul O1 și O2 pentru a efectua intersecția directă cu cercuri și m2 și m1 obține punctul de cuplare A și B. Între aceste puncte și conjugare efectuate arc de cerc cu raza R centrat la O.

(. Figura 33) Atunci când conjugare mixtă cuplarea centrului O este definit la intersecția a două loci - cercuri auxiliare de raze R + R1 și R-R2. a avut loc, respectiv, din centrele O1 și O2. cuplare punctele A și B se afla la intersecția centrelor OO1 de linii și arce cu cercuri oo2 date.

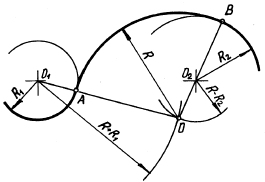
Fig. 33. Construcția de cuplare mixtă a două cercuri

Construirea de linii de tangenta

Construcția de tangentelor la cercuri se bazează pe faptul că linia tangentă perpendicular pe raza unui cerc efectuat la punctul de tangență.

Construirea de tangenta la cercul de la punctul A situată în afara cercului (Fig. 34). Segment OA conectarea punct dat A cu centrul cercului O, divide în jumătate și din punctul obținut O1. ca centru, descrie un cerc cu o rază auxiliară O1 A. auxiliara cerc predeterminat se intersectează în punctul B, care este punctul de tangență. AB Direct va fi tangenta la cercul, ca ABO unghi drept, ca scriere cercului auxiliar și bazat pe diametrul său.

Construcția unei tangente la cele două cercuri. Tangenta la cele două cercuri pot fi externe, dacă ambele cercuri sunt dispuse pe o parte a acesteia, iar circumferința interioară dacă sunt localizate pe părți diferite ale tangenta.

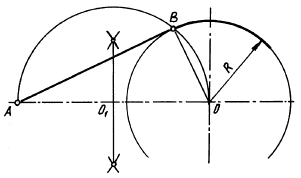
Fig. 34. Construcția unei tangente la un cerc

Pentru a construi o tangentă la circumferințele exterioare ale razelor R1 și R2 vom proceda după cum urmează (Figura 35.):

1). Centrul de O2 mai mare circumferință conduce auxiliar raza cercului R2 -R1;

2). O1 O2 se taie în jumătăți;

3). cu centrul O3 efectuează cerc auxiliar cu o rază de O2 O3;

4). Menționăm punctele de intersecție a două cercuri auxiliare - M și N;

5). prin punctul O2 și punctul obținut efectuează linii până la intersecția cu cercul de rază R2. Obținem punctele B și D;

6). din centrul O1 O1 efectuarea liniilor A și C, respectiv paralele O1 O2 și O2 în D până la intersecția cu cercul de rază R1 la punctele A și C.

AB directă și CD - a căutat tangente externe la două cercuri.

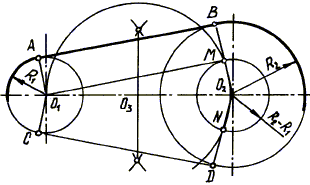
Fig. 35. Construcția tangenta exterior la două cercuri

Construcție tangent interior la cele două cercuri de raze R1 și R2 (Fig. 36).

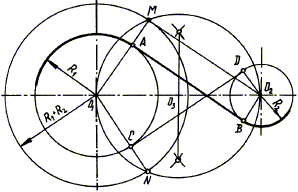
Fig. 36. Construcția tangenta interne a două cercuri

Din centrul unuia dintre cercuri, de exemplu O1. efectuarea auxiliare raza cercului R1 + R2. Se împarte segmentul O1 O2 jumătate și din punctul care rezultă O3 oa doua rază de cerc auxiliar O1 O3. Punctele M și N intersecția filială a cercurilor conectate printr-o O1 dreaptă cu centru și la intersecția lor cu cercul de rază R1 obține punctul tactil A și C. De la O2 conduce linia O1 paralelă obține A și în contact cu punctul B pe un cerc R2. În mod similar construit punctul D. Direct AB și CD - dorit tangente interne la cele două cercuri.