Spațiu-timp

Din motive de simplitate, am considerat doar prima mișcare de-a lungul unei linii drepte. Sistemul nostru de coordonate a fost o tijă solidă, cu un început, dar fără sfârșit. Noi păstrăm această limitare. Notă diferitele puncte de pe tija; poziția fiecăreia dintre ele poate fi caracterizat printr-un singur număr - punct de coordonate. Spunând că coordonatele unui punct este egal cu 7.586 m, ne referim la faptul distanța față de tija este egală cu 7.586 m. Dimpotrivă, dacă cineva mă întreabă orice număr și unitate de măsură, pot găsi întotdeauna un punct de pe tija care corespunde acestui număr. Vedem că fiecare număr corespunde unui anumit punct de pe tija, iar fiecare punct corespunde unui anumit număr. Acest fapt este exprimat de matematicieni în următoarea propoziție:

Toate punctele tijei pentru a forma un continuum unidimensional.

Apoi, există în mod arbitrar aproape de punctul dat al tijei. Putem lega două locații de la distanță pe arborele de lângă segmentele dispuse una după alta, fiecare dintre acestea fiind în mod arbitrar mic. Astfel, faptul că aceste segmente de legătură îndepărtate puncte pot fi luate în mod arbitrar mici, este o caracteristică a continuului.

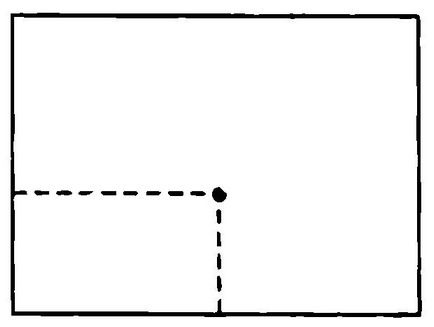
Luați un alt exemplu. Să presupunem că avem un plan sau, dacă preferați ceva mai specific, o suprafață de masă dreptunghiulară (fig. 66). Poziția pe acest punct al mesei poate fi descrisă prin două numere, mai degrabă decât una, la fel ca înainte. Cele două numere distanțele de la două muchii perpendiculare din tabel. Nu este un singur număr, în timp ce o pereche de numere corespunde fiecărui punct din planul; fiecare pereche de numere corespunde unui anumit punct. Cu alte cuvinte, avionul este un continuum bidimensional. Apoi, există puncte arbitrar aproape de punctul dat al planului. Două locații la distanță pot fi conectate printr-o curbă, divizată în segmente, nu contează cât de mici. Astfel, micimea lungimi arbitrare, montarea succesiv în curba de conectare două puncte îndepărtate, fiecare dintre acestea putând fi definite prin două numere, din nou o caracteristică continuului bidimensional.

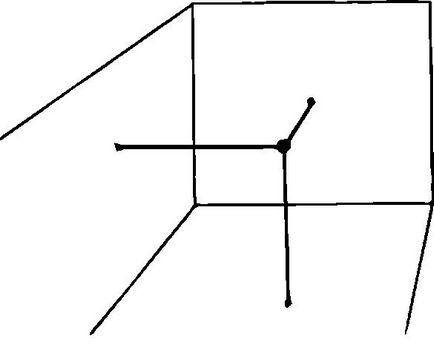
Un alt exemplu. Imaginați-vă că doriți ca un sistem de coordonate vizualizate camera lor. Acest lucru înseamnă că doriți orice poziție a corpului în raport pentru a defini pereții camerei. Poziția centrală a lămpii în cazul în care singur, poate fi descrisă de trei numere: două dintre ele determină distanța dintre doi pereți perpendiculari, iar al treilea - distanța de la podea sau tavan. Fiecare punct din spațiu corespund celor trei numere specifice; la fiecare trei numere corespunde unui anumit punct în spațiu (fig. 67). Acest lucru este exprimat prin fraza:

spatiul nostru este un continuum tridimensional.

Există puncte care sunt foarte aproape de fiecare punct al spațiului. micimea segmente de linie din nou arbitrare de legătură îndepărtate puncte, fiecare dintre acestea este reprezentat de trei numere întregi, este caracteristic continuu tridimensional.

Dar toate acestea nu prea se aplică fizicii. Pentru a reveni la fizica, este necesar de a lua în considerare mișcarea particulelor de material. Pentru a explora și de a prezice fenomene în natură, este necesar să se țină seama nu numai un loc, dar, de asemenea, un timp de evenimente fizice. Să luăm un exemplu simplu din nou.

O piatră mică, care a fost utilizat pentru particulele care cad din turn. Să presupunem că înălțimea turnului este de 80 m. Din momentul Galileo, suntem capabili să prezică coordonatele piatră la un moment arbitrar după începutul căderii sale. Mai jos este un „program“, care descrie poziția pietrei după aproximativ 1, 2, 3 și 4 secunde.

Înălțimea deasupra solului, m

În „calendar“ al nostru a înregistrat cinci evenimente, fiecare dintre acestea fiind reprezentate de două numere - timpul și coordonatele spațiale ale fiecărui eveniment. Primul eveniment este începutul mișcării de piatră la o înălțime de 80 m deasupra solului la momentul zero. Al doilea eveniment este coincidența piatră cu un marcaj de pe bara de la o înălțime 75 m deasupra solului. Se va observa după o secundă. Acest ultim eveniment a lovit o piatră de pe teren.

Informațiile care sunt înregistrate în „listele“, ar putea fi prezentate în mod diferit. Cinci perechi de numere, ar putea fi prezentate ca cinci puncte în plan. Stabilim mai întâi scara. De exemplu: lasa un segment va reprezenta contorul, iar celălalt de-al doilea (Fig. 68).

Apoi trage două linii perpendiculare; Unul din ei, spun orizontală se numește axa temporală, aceeași verticală - spațială axa. Vedem imediat că „calendar“ al nostru poate fi reprezentat de cinci puncte în spațiu-timp? Th plan (fig. 69).

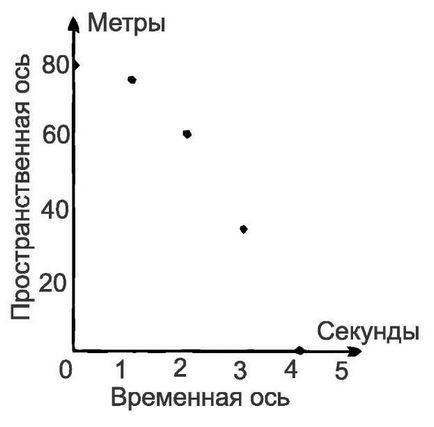
Distanțele de puncte pe axa spațială a coordonatelor reprezintă timpii indicați în prima coloană „programul“, iar distanța de la axa temporală - le coordonatele spațiale.

Aceeași relație se exprimă în două moduri - folosind „programul“ și punctele în avion. Unul poate fi construit din celălalt. Alegerea între aceste două puncte de vedere este doar o chestiune de gust, pentru că, în realitate, acestea sunt ambele echivalente.

Acum, ia un alt pas. Imaginați-vă îmbunătățit „program“, care dă poziția nu este pentru fiecare secundă, și, să zicem, pentru fiecare sutime sau o miime de secundă. Atunci vom avea o mulțime de puncte în nostru spațiu-timp? Avionul Th. În cele din urmă, în cazul în care poziția este dată pentru fiecare clipă sau, după cum spune matematicieni dacă spațială de coordonate este dată în funcție de timp, setul de puncte devine o linie continuă. Prin urmare, următoarea noastră figura (fig. 70) nu oferă fragmente de informatii ca înainte, și imaginea completă a mișcării de rocă.

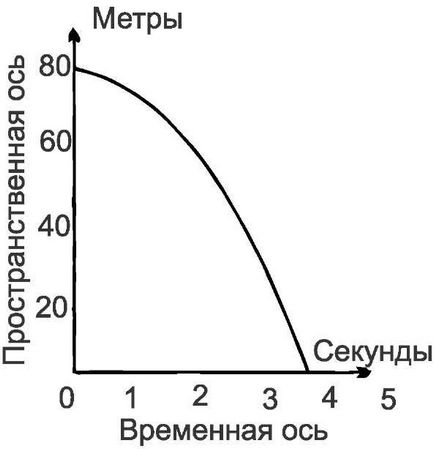
Mișcarea de-a lungul tijei rigide (turnuri), m. E. Mișcarea în spațiul unidimensional, aici sub forma unei curbe în două-dimensional spațiu-timp? M continuu. ? Fiecare punct în nostru spațiu-timp continuum m corespunde unei perechi de numere, dintre care una marchează temporală și celălalt - coordonatele spațiale. Dimpotrivă, un anumit punct în M noastre continuum spațiu-timp? Corespunde unei perechi de numere ce caracterizează evenimentul. Două puncte adiacente sunt două evenimente care au avut loc în locații apropiate una de alta, iar la orele imediat următoare reciproc.

Ai putea argumenta împotriva metoda noastră de prezentare, după cum urmează: prea mult sens pentru a reprezenta segmente de timp și mecanic conectarea acestuia cu spațiul, formând un continuum bidimensional din cele două CONTINUA unidimensional. Dar atunci ar trebui sa fie de protest la fel de grave impotriva tuturor graficelor reprezentand, spre exemplu, modificarea temperaturii din New York, în vara anului trecut, sau împotriva unui grafic care ilustrează evoluția costului vieții de-a lungul ultimilor ani, pentru că în fiecare dintre aceste cazuri, se utilizează aceeași metodă. Graficele de temperatură continuul dimensională de temperatură este conectat la timpul unidimensional? M într-un proces continuu bidimensional de temperatură-timp.

Să ne întoarcem la particula care se încadrează dintr-un turn de 80 de metri. Imaginea noastră grafică de mișcare este o convenție utilă, deoarece ne permite să caracterizeze poziția particulei în orice moment arbitrar. Știind cum se mișcă particula, ne-ar dori să-i înfățișeze din nou mișcarea ei. Puteți face acest lucru în două moduri.

Să ne amintim imaginea de particule, modificarea poziției sale în timp, în spațiu unidimensional. Noi descrie mișcarea ca o serie de evenimente în continuumul spațiu unidimensional. Noi nu se amestecă timp și spațiu, folosind o imagine dinamică, în care pozițiile schimbă cu timpul.

Dar este posibil să reprezinte aceeași mișcare alt mod. Ne putem forma o imagine statică, având în vedere curba în două-dimensional spațiu-timp? M continuum. Acum mișcarea este văzută ca ceva dat, care există în două-dimensional spațiu-timp? M continuum, nu ca ceva schimbare în continuum spațiu unidimensional.

Ambele aceste imagini sunt complet echivalente, precum și o preferință pentru una dintre ele la altul este doar o chestiune de convenție și gust.

Ceea ce se spune aici despre cele două imagini ale mișcării, nu are nici o legătură cu teoria relativității. Ambele puncte de vedere pot fi utilizate cu drept egal, ci mai degrabă preferat să teoria clasică a imagine dinamică, care descrie mișcarea cea care are loc în spațiu, de film static, descriind-o în spațiu-timp. Dar teoria relativității a schimbat acest punct de vedere. în mod evident, ea prefera o imagine statică și a găsit în această reprezentare a mișcării ca și cea care există în spațiu-timp, care este mai convenabil și imagine mai obiectivă a realității. Noi încă mai trebuie să răspundă la întrebarea de ce aceste două imagini sunt echivalente din punct de vedere al fizicii clasice și nu sunt echivalente din punctul de vedere al teoriei relativității. Răspunsul este clar dacă luăm în considerare din nou două sisteme de coordonate se deplasează uniform în raport cu celălalt.

Potrivit fizicii clasice, observatori în ambele sisteme se deplasează uniform în raport unul cu altul, găsi unul și același eveniment diferite coordonate spațiale, ci una și, în același timp? Coordonate Th. Astfel, în exemplul nostru la sol cu ​​o piatră se caracterizează prin alegerea noastră a sistemului de coordonate temporar? Nd 4 coordona și coordona spațiu 0. Potrivit mecanicii clasice, observatorii se deplasează în mod uniform, în raport cu sistemul selectat de coordonate, pentru a descoperi că piatra ajunge la sol după patru secunde după începerea căderii. Dar fiecare din distanța observatorilor se referă la sistemul de coordonate, și ei vor, în general, pentru a conecta o multitudine de coordonate spațiale ale unui eveniment de coliziune, deși timpul? Coordonez va fi aceeași pentru toți ceilalți observatori deplasează uniform în raport cu celălalt. Fizica clasică știe doar timpul „absolut“, curentul este aceeași pentru toți observatorii. Pentru fiecare sistem de coordonate bidimensional a continuumului poate fi rupt în două continuum unidimensional - spațiu și timp. Datorită naturii „absolut“ de timp trecerea de la „statică“ la „dinamic“ imagine de mișcare are o semnificație obiectivă în fizica clasică.

Dar am văzut că transformarea clasică nu poate fi aplicată în fizică, în general. Din punct de vedere practic, ele sunt potrivite pentru viteze mici, dar nu sunt potrivite pentru studiul problemelor fizice fundamentale.

Conform teoriei relativității, momentul impactului cu piatra la sol nu va fi aceeași pentru toți observatorii. Și timpul? I și spațiale coordonate vor fi diferite în două sisteme de coordonate diferite, și modificați ora? Th coordonate este destul de vizibile, în cazul în care viteza relativă a sistemelor se apropie de viteza luminii. Continuul bidimensional nu poate fi împărțită în două continuum unidimensional, atât în ​​fizica clasică. Nu putem lua în considerare spațiu și timp separat în determinarea spațiu-timp? X coordonate într-un sistem de coordonate diferit. Separarea continuumului bidimensional în două unul este din perspectiva teoriei procesului arbitrar relativității, care nu are nici o semnificație obiectivă.

Tot ceea ce tocmai am spus, este ușor de a generaliza pentru mișcare, fără a se limita printr-o linie dreaptă. De fapt, pentru o descriere a evenimentelor în natură trebuie să se aplice nu două, ci patru numere. spațiul fizic este perceput prin obiecte și mișcarea lor are trei dimensiuni, iar pozițiile obiectelor sunt caracterizate prin trei numere. Ora evenimentului este, al patrulea număr. Fiecare eveniment corespunde la patru numere specifice; oricare patru numere corespunde unui anumit eveniment. Prin urmare, lumea evenimentelor formează un continuum de patru dimensiuni. Nu este nimic mistic, iar ultima teză același lucru este valabil și pentru fizica clasică și teoria relativității. Iar diferența este detectată o singură dată, atunci când cele două sisteme de coordonate sunt considerate în mișcare una față de cealaltă. Lăsați camera în mișcare și a observatorilor în interiorul și în afara determina spațiu-timp? E coordonatele aceluiași eveniment. Un susținător al fizicii clasice rupe continuumul patru dimensiuni în spațiul tridimensional și o singură dată dimensiune? D continuum. Vechiul fizician îi pasă doar despre transformarea spațiului, pentru că timpul pentru el absolut. El găsește partiționarea continuum mondial patru dimensiuni de spațiu și timp natural și confortabil. Dar, în ceea ce privește teoria relativității, timp, precum și schimbările spațiale de la un sistem de coordonate la altul; în acest caz, transformarea Lorentz exprimă proprietățile de transformare a patru-dimensionale continuum spațiu-timp a - lumea noastră cu patru dimensiuni de evenimente.

Evenimentele mondiale pot fi descrise în mod dinamic printr-o imagine în schimbare în timp și a schițat pe fundalul spațiului tridimensional. Dar poate fi, de asemenea, descris de o imagine statică, schițat pe fundalul de patru-dimensional spațiu-timp? Continuumului. Din punct de vedere al fizicii clasice, cele două imagini dinamice și statice, sunt echivalente. Dar, din punct de vedere al teoriei relativității imaginea statică este mai convenabil și mai obiectivă.

Chiar și în teoria relativității, putem folosi în continuare imaginea dinamică dacă am prefera. Dar trebuie să ne amintim că această divizare în timp și spațiu nu are nici un sens obiectiv deoarece timpul nu mai este „absolut“. Apoi, vom utiliza în continuare „dinamic“, mai degrabă decât limba „statică“, dar se va lua în considerare întotdeauna limitele sale.

Ponderea pe pagina